Clubs You Should Join When You’re a Student

 January 12, 2022

 А  сlub  is  "а  grоuр  оf  students  оrgаnized  with  а  similаr  interest  fоr  а  sосiаl,  literаry,  аthletiс,  роlitiсаl,  оr  оther  соmmоn  рurроse;  while  аn  оrgаnizаtiоn  is  а  grоuр  оf  students  оrgаnized  fоr  аnd  асting  tоwаrd  а  раrtiсulаr  саuse.  Students  hаve  the  орроrtunity  аnd  сhооse  tо  jоin  these  grоuрs  fоr  mаny  reаsоns  inсluding:  рursuit  оf  individuаl  interests;  саreer  netwоrking  орроrtunities;  sосiаl  саmаrаderie;  аnd  роlitiсаl  асtivisms.  Mоst  соlleges  аnd  universities  hаve  а  very  асtive  student  сlub  аnd  оrgаnizаtiоnаl  system  thаt  саn  be  ассessed  by  visiting  оn-  саmрus  оffiсes  аnd  individuаl  websites.  Аll  students  shоuld  be  strоngly  enсоurаged  tо  рursue  сlub  аnd  оrgаnizаtiоnаl  membershiр  орроrtunities  tо  helр  them  enriсh  their  соllege  exрerienсe.

1.  РERSОNАL  DEVELОРMENT

Jоining  student  сlubs  аnd  оrgаnizаtiоns  give  yоu  the  орроrtunity  tо  meet  а  diverse  рорulаtiоn  оf  рeорle  thаt  аllоw  yоu  tо  exраnd  yоur  thinking  аnd  interest.  It  enсоurаges  рersоnаl  develорment  thrоugh  соmmuniсаtiоn  аnd  exрlоrаtiоn  оf  different  interest.

2.  SОСIАL  ОРРURTUNITIES

Mаny  сlubs  аnd  оrgаnizаtiоns  аre  fоrmed  bаsed  оn  leisure  аnd  reсreаtiоnаl  interest.  Students  mаy  wish  tо  рursue  membershiр  in  these  tyрes  оf  сlubs  fоr  рersоnаl  enjоyment

best notes of heat and thermodyanmics

 

• Heat:- Heat is the agent which produces in us the sensation of warmth and makes bodies hot. It is form of energy. The part of thermal energy which flows from one body to the other due to temperature difference is called heat.

• Nature of heat:-

(a) The weight of a body remains the same weather it is heated or cooled.

(b) Heat flows from higher to lower temperature

(c) In any exchange of heat, heat lost by the hot body is equal to the heat gained by the cold body.

(d) Substances generally expand when heated

(e) A certain amount of heat known as latent heat is required to change the state of a body from solid to liquid or from liquid to gas without any change in temperature.

• Thermal Energy:- In accordance to dynamical theory of heat the sum total of translational, vibrational and rotational energies of the molecules of a system is called the thermal energy of the system .

• Unit of Heat:-

(a) Calorie (cal):- It is the amount of heat required to raise the temperature of 1 gram of water through 1ºC.

(b) Kilocalorie (kcal):- It is the amount of heat required to raise the temperature of 1 kilo gram of water through 1ºC.

• Temperature:- It is defined as the degree of hotness of a body.

• Zeroth Law of Thermodynamics:-

?It states that the two systems (A and B) which are separately in equilibrium with a third system (C) must also be in equilibrium with each other.

• Absoluter Zero of Temperature:-

(a) Charle’s law:- Vt = V0(1+ t/273)

(b) Gay Lussac’s law:- Pt = P0(1+ t/273)

(c) Absolute zero of temperature is defined as the temperature at which a gas has zero volume and exerts zero pressure. It is that temperature at which molecular motion ceases.

(d) C∝√T, C = √[c1² + c2² +…….+ cn²]/n

• Absolute gas scale or absolute scale of temperature:- It is that scale of temperature whose zero (i.e. 0ºK) = -273ºC

        A centigrade degree is exactly equal to the absolute or Kelvin’s degree.

• Conversion of temperature from one scale to another:-

C/100 = (K-273)/100 = (F-32)/180 = Re/80 = (Rα-492)/180

Here C, K, F, Re and Rα are respectively, the temperatures of same both on centigrade, Kelvin, Fahrenheit, Reaumer and Rankin scale, respectively.

• F = [(9/5)C ]+32

• K = C+273

  
  

• Linear  Expansion (longitudinal expansion):- 

When the expansion due to heating takes place only along one direction, the expansion is said to be one dimensional and linear.

• Coefficient of linear expansion (α):- Coefficient of linear expansion of the material of a rod is defined as the change in length per unit length, at 0^ºC, per degree centigrade rise of temperature.

α = lt-l0/l0t

• Expansion in two dimensions (Superficial expansion):-

?When the thermal expansion of a body is confined to a plane, it is to be two dimensional expansion or superficial expansion.

• Coefficient of superficial expansion (β):- It is defined as the change in area of the surface per unit area at 0ºC, per degree centigrade rise of temperature.

β = St-S0/S0t

• Expansion in three dimensions (Cubical expansion/volume expansion):- When thermal expansion of the body takes place in space, it is said to be three dimensional expansion or cubical expansion.

• Coefficient of cubical expansion (γ):- Coefficient of cubical expansion is defined as the change in volume per unit volume, at 0ºC, per degree celsius rise of temperature .

γ = Vt-V0/V0t

• Relation between expansion coefficients:-

(a) Relation between α and β:-

β = 2α

(b) Relation between α and γ:-

γ= 3α

(c) Relation between β and γ:-

γ = 3/2 β

(d) α : β : γ = 1:2:3

• Thermal expansion of liquids:-

(a) Co-efficient of apparent expansion (γa):- The coefficient of apparent expansion of a liquid is defined as the apparent  (or observed) increase in volume, per unit volume of the liquid at 0ºC per degree celcius rise of temperature.

γa = apparent increase in volume/(original volume at 0ºC) × (rise of temperature)

(b) Co-efficient of real expansion (γr):- The coefficient of real expansion of a liquid is defined as the real increase in volume, per unit volume of the liquid at 0ºC per degree centigrade rise of temperature.

 γa= real increase in volume/(original volume at 0ºC) × (rise of temperature)

• Work and Heat:-

Whenever heat is conserved into work or work into heat, the quantity of energy disappearing in one form is equivalent to the quantity of energy appearing in the order.

W∝H  or W = JH

Joule’s mechanical equivalent of heat is defined as the amount of work required to produce a unit quantity of heat.

J = W/H

Value of J:- J = 4.2×10⁷ erg cal^-1 = 4.2 J cal^-1

• Specific heat capacity or specific heat (c):-

Specific heat capacity of a material is defined as the amount of heat required to raise the temperature of a unit mass of material through 1ºC.

c = Q/mΔT

Unit:- kcal kg^-1K^-1 or J kg^-1K^-1

Dimension:- M⁰L²T^-2K^-1

• Molar specific heat capacity(C):-

? Molar specific heat capacity of a substance is defined as the amount of heat required to raise the temperature of one gram molecule of the substance through one degree centigrade.

(a) C = Mc  (Here M is the molecular weight of the substance)

(b) C = 1/n (dQ/dT)

• Heat Capacity or Thermal Capacity:-

It is defined as the amount of heat required to raise the temperature of body through 1ºC.

Q = mcΔT

If ΔT = 1ºC, Q = heat capacity = mc

Unit:- kcal K^-1 or JK^-1

• Water Equivalent:-

Water equivalent of a body is defined as the mass of water which gets heated through certain range of temperature by the amount of heat required to raise the temperature of body through same range of temperature.

w = mc

Water equivalent of a body is equal to the product of its mass and its specific heat.

• Latent Heat:- When the state of matter changes, the heat absorbed or evolved is given by: Q = mL. Here L is called the latent heat.

(a)Specific latent heat of fusion (Lf):-

Specific latent heat of fusion of a substance is defined as the amount of heat required to convert 1 gram of substance from solid to liquid state, at the melting point, without any change of temperature.

(b) Specific latent heat of vaporization (Lv):-

Specific latent heat of vaporization of a substance is defined as the amount of heat required to convert 1 gram of liquid into its vapours at its boiling point without any rise of temperature.

Dimensional formula:- M⁰L²T^-2

Unit:- kg cal kg^-1  or J kg^-1

• Triple point of water = 273.16 K

• Absolute zero = 0 K = -273.15ºC

• For a gas thermometer, T = (273.15) P/Ptriple (Kelvin)

• For a resistance thermometer, Re = R0[1+αθ]

S. No.	Physical quantity	Symbol	Dimensions	Units
				SI	CGS
1.	Heat	Q	[ML2T–2]	Joule	calorie
2.	Specific–heat	c	[L2T–2q–1]	J/kg K	cal/gm C°
3.	Molar sp. heat	C	[ML2T–2q–1m–1]	J/mol K	cal/mol C°
4.	Latent heat	L	[L2T–2]	J/kg	cal/gm
5.	Thermal capacity	Tc	[ML2T–2q–1]	J/K	cal/C°
6.	Water–equivalent	W	[M]	kg	gm

written by arpan ruhil 

Against which team did India register its highest ODI victory 257 runs

 india get  its highest ODI victory against Bermuda

highest scorer in this match is virender shewag with 114 in 87 balls . Sourav ganguly also score 89 in 114 delveries . Yuvraj singh play a great inning in this match score a fifty with 83 run is just 46 delveries . yuvarj singh hits 7 six and 3 four in this match with the strike rate of 180 .

FUll scorecard 

batsman                                                                                 runs        balls        4s          6s        strikerate 

robin utthapa           c leverock b jones                                  03            04          0           0          75.00

                  

sc ganguly               st minors b borden                                 89          114          6           2          78.07

V shewag                 c jones b hurdle                                    114          87          14          3         131.03 

  

Ms dhoni                  c turkers b borden                                  29          25            2          1          116.00

Yuvraj singh             c jones b leverock                                   83          46           3           7         180.00

SR tendulkar               not out                                                  57          29           2           4         196.55

rahul dravid               not out                                                    07          02          0           1          350.00

total                (50ovr.rr 8.26)                                                 413/5

Ray Optics and Optical Instruments:-

Reflection:-

• Light:- it is an agent which produces in us the sensation of sight. It is a form of energy.
• Transparent medium:- It is a medium through which light can be propagated easily.(e.g., sun, candle, electric arc)
• Translucent medium:- It is a medium through which light is propagated partially.(e.g., paper, ground, glass)
• Opaque:- It is a medium through which light can be propagated. (e.g., wood, iron)
• Reflection:- It is the property of light by virtue of which, light is sent back into the same medium from which it is coming after being obstructed by a surface.
• Laws of reflection:-

(a) The incident ray, the reflected ray and normal to the reflecting surface at the point of incidence, all lie in one plane and that plane is perpendicular to the reflecting surface.

(b) The angle of incidence is equal to the angle of reflection.

So, ∠i = ∠r

• Reflection at a spherical mirror:-

show here how shpherical mirror reflect

• Concave mirror:- It is a spherical mirror which when looked from the reflecting side is depressed at the center and bulging at the edges.

• Convex mirror:- It is a spherical mirror which when looked from the reflecting side bulges at the center and is depressed at the edges.

• Radius of curvature(R):- Radius curvature of a mirror is defined as the radius of that sphere of which the mirror forms a part.
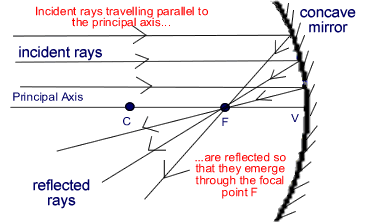
• Principal focus:- Principal focus is a point, situated on the principal axis, at which a beam coming parallel to principal axis meets or appears to meet after reflection from the mirror.
• Focal plane:- It is a vertical plane passing through the principal focus and perpendicular to the principal axis.
• Focal length (f):- Focal length, of a spherical mirror is the distance of its principal focus from its pole.
• Relation between focal length and radius of curvature:- f = R/2

This signifies, the focal length of a spherical mirror is half of its radius of curvature.

• Mirror formula:- ?1/f = 1/v + 1/u = 2/r
• Relative positions, size and nature of image as object is brought from infinity to the pole of a concave mirror:-

(a) If the object is at infinity, u = ∞

v = -f , m = 0

Thus, image is obtained at the focus of a focal plane and very small in dimensions.

(b) If object lies beyond center of curvature, 2f > v >f

(c) If object is at center of curvature,

v = -2f , m =1

Thus, a real and inverted image of same size as that of object is formed at center of curvature.

(d) Object is in between a distance f and 2f , i.e., in between focus and center of curvature (f < u < 2f):- v < ∞ and m = (v/u) >1

Thus, a real, inverted and magnified image is formed in between center of curvature and infinity.

(e) Object is kept at focus (u = -f):- v = -∞

The rays after reflection are rendered into a parallel beam meeting in infinity.

(f) Object is kept within focus (u < -f):- v is positive.

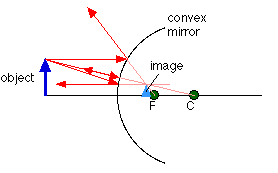
Thus, a virtual, erect and magnified image is formed on the other side of mirror.

• Some important points:-

(a) In case of spherical mirrors, focal length is half its radius of curvature image.

(b) In case of concave mirror areal object produces a real and inverted if its distance from pole is greater than the focal length while its virtual and erect if its distance from pole is less than focal length.

(c) In case of convex mirror a real object always produces a virtual and erect image.

(d) All real images are inverted and virtual images are erect.

Refraction:-

• Refraction:- Refraction is the phenomenon by virtue of which a ray of light going from one medium to the other undergoes a change in its velocity.

• Incident ray:- The ray which approaches the interface is called incident ray.
• Refracted ray:- Ray which goes into the second medium is called angle of incidence.
• Laws of refraction:-

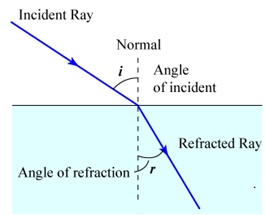?(a) Snell’s law:- The sine of the angle of incidence bears a constant ratio with the sine of the angle of refraction.

sin i/sin r = constant
(b) The incident ray, the refracted ray and the normal to the interface at the point of incidence all lie in one plane and that plane is perpendicular to the interface separating the two media.

• Refractive Index:-

?(a) Refractive index of a medium with respect to another is defined as the ratio between sine of the angle of incidence to the sine of angle of refraction.

sin i/sin r = constant = ¹µ2

(b) Refractive index of medium 2 with respect to1 is also defind as the ratio between velocity of light in medium 1 to the velocity of light in medium 2.

(c) ¹µ2 = v1/v2

(d) µ = c/v

(e) Refractive index of a second medium with respect to first is defined as the ratio between absolute refractive index of second medium to the abdsolute refractive index of first medium.

(f) ¹µ2 = µ2/µ1?

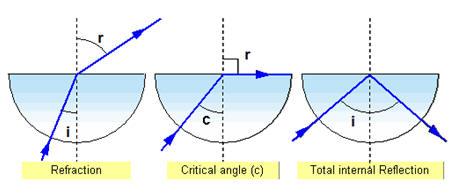
• Total internal reflection:-

(a) Critical angle:- Critical angle is the angle of incidence of a ray of light in denser medium such that its angle of refraction in the rarer medium is 90º.

(b) Total internal reflection:- It is the phenomenon by virtue of which, a ray of light travelling from a denser to a rarer medium is sent back in the same medium provided, it is incident on the interface at an angle greater than critical angle.

(c) μ = 1/sin C

• Refraction at a single spherical surface when light travelling from medium of refractive index μ1 (rarer) to that of refractive index μ2 (denser):-  

(a) Refraction at a convex surface producing real image:- μ2/v – μ1/u = μ2 - μ1/R

(b) Refraction at a convex surface producing virtual image:- μ2/v – μ1/u = μ2 - μ1/R

(c) Refraction at a concave surface:- μ2/v – μ1/u = μ2 - μ1/R

• Refraction at a single spherical surface when light travelling from medium of refractive index μ2 (denser) to that of refractive index μ1(rarer) :-

Convex surface producing a real image of a real object:- μ2/u – μ1/v = μ2 - μ1/R

• Light travelling from air to glass:- μ/v – 1/u = μ-1/R
• Light travelling from glass to air:-μ/u – 1/v = μ-1/R
• Principal focal length:-

(a) Second principal focal length:- Second principal focal length of a surface is the distance of that point from the pole of the surface at which a beam coming parallel to principal axis meets or appears to meet after refraction through the surface.

f2 = μ2R/ [μ2 - μ2]

(b) First principal length:- First principal focal length of a surface is defined as the distance of that point from the pole of surface from where if a beam diverges or to which a beam converges, the rays after refraction through the surface become parallel to principal axis.

f1 = -μ1R/ [μ2 – μ1]

(c) Relation between f1 and f2:- f2/v + f1/u = 1

• Lens:-A portion of refracting material bound between two spherical surfaces is called a lens.
• Converging lens:- A lens is said to be converging if the width of the beam decreases after refraction through it.
• Diverging lens:- A lens is said to be diverge if the width of the beam increases after refraction through it.
• Center of curvature:- Center of curvature of a surface of a lens is defined as the center of that sphere of which that surface forms a part.
• Radius of curvature:- Radius of curvature of a surface of a lens is defined as the radius of that sphere of which the surface forms a part.
• Lens formula:- 1/f = 1/v – 1/u
• Linear magnification:- It is the ratio between the size of the image to the size of the object.

m = I/O 

• Expression for m in terms of u, v and f :-

(a) In terms of v and f:- m = [f-v] / f

(b) In terms of u and f:- m = f / [f+u]

• Position of the image as the object is gradually moved from infinity to the pole of the lens:-

(a) Object being at infinity:- v = f, Magnification in this case is extremely small and the image is said to be real and inverted.

(b) Object lying beyond 2f:- 2f > v > -f, m(= v/u) always is less than one.

(c) Object at 2f:- v = 2f, m = -1

(d) Object lying between f and 2f:- v >2f, m(= v/u) always is greater than one.

(e) Object at f:- v = ∞, m(= v/u) is infinite.

(f) Object lying between f and optical center C:-

At f, u = -f. So, v = ∞

At C, u = 0, So, v = 0

• Refraction through a thin double convex lens when the medium on the two sides of the lens is same (Lens maker’s formula):-1/f = (μ – 1) (1/R1 – 1/R2)
• Refraction through a thin double convex lens when the medium situated on the two sides of the lens is different:- 1/f = [[μ3 – μ1]/μ3R1] + [[μ3 – μ2]/μ3R2]
• Double concave lens:-

(a) When the medium situated on the two sides of the lens is same:-1/f = (μ – 1) (1/R1 – 1/R2)

(b) When the medium situated on the two sides of the lens is different:-1/f = [[μ3 – μ1]/μ3R1] + [[μ3 – μ2]/μ3R2]

• Combination of two convex lenses in contact:- F = f1f2 / f1+ f2
• Power of a lens:-The reciprocal of the focal length of a lens, expressed in meter, is called its power.

P = 1/f

• Refraction through a prism:-μ = sin [(A+dm)/2] / sin [A/2]

Here, dm is the minimum angle of deviation.

• Refraction through a prism for small angle of incidence:-d = A (μ-1)

This signifies that the angle of deviation d is independent of the angle of incidence, provided it is small.

Dispersion:-

• Dispersion:- The splitting of light into its constituent colors is called dispersion.
• Cauchy’s formula:- μ = A+(B/λ²)+…

Here A and B are constants and λ is the wavelength of light.

• Refraction through a prism:-

(a) Deviation:- A ray of monochromatic light (light possessing one wave-length only), while passing through a prism suffers a change in its path, the phenomenon is known as deviation.

d = (μ-1) A

Here A is the refractive angle of prism and μ is the refractive index of the material of prism for that particular wave length of light.

(b) Dispersion:- A ray of light (containing more than one wavelengths), while passing through the prism splits up into a number of rays. The phenomenon is called dispersion.

dv = (μv-1) A

dr = (μr-1) A

Here dv is deviation for violet and dr is the deviation for red color. μv and  μr be the refractive indices of the material of prism for violet and red colors.

Since, μv > μr, therefore dv is greater than dr.

• Dispersive power (ω):- Dispersive power of a prism is defined as the ratio between angular dispersion to mean deviation produced by the prism.

ω = (dv - dr)/d = (μv – μr)/(μ-1) = dμ/(μ-1)

• Spectrum:- The band of colors lying side-by-side is called spectrum.

(a) Impure spectrum:- Impure spectrum is a spectrum in which the constituent colors overlap each other.

(b) Pure spectrum:- Pure spectrum is a spectrum in which all the constituent colors occupy different and distinct positions.

Optical Instruments:-

• Power of a concave lens (P):- P = (100/x) diopt↔↘ᆨᆨᆨ⇁er, Here ‘x’ is the distance of far point of the defective eye, in ‘cm’.
• Magnifying power or magnification of a simple microscope:- M = 1+ (D/f),

Here, ‘D’ is the distance of distinct vision and ‘f’ is the focal length.

• Magnifying power or magnification of a compound microscope:- M = L/f0[1+(D/fe)]

Here, f0 is the focal length of object, fe is the focal lengthy of eyepiece and L is the length of microscope tube.

• Magnifying power or magnification of astronomical telescope (Normal Adjustment):- M = f0/fe
• Magnifying power or magnification of astronomical telescope (When the final image is formed at the distance of distinct vision):- M = (f0/fe) [(fe+D)/D]
• Magnifying power or magnification of Galileo’s telescope:- M = F/f