- Rigid Body:- A rigid body consists of a number of particles confined to a fixed geometrical shape and size in such a way that the distance between any pair of particles always remains constant.
- Cross Product (Vector Product):- Cross product of two vectors
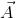 and
and 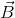 1is defined as a single vector
1is defined as a single vector  whose magnitude is equal to the product of their individual magnitudes and the sine of the smaller angle between them and is directed along the normal to the plane containing
whose magnitude is equal to the product of their individual magnitudes and the sine of the smaller angle between them and is directed along the normal to the plane containing 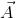 and
and 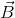 .2
.2
Here  is the unit vector in a direction perpendicular to the plane containing
is the unit vector in a direction perpendicular to the plane containing 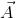 and
and 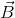 .3
.3
 is the unit vector in a direction perpendicular to the plane containing
is the unit vector in a direction perpendicular to the plane containing 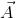 and
and 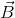 .3
.3- Centripetal force:- The force, acting along the radius towards the center, which is essential to keep the body moving in a circle with uniform speed is called centripetal force. It acts always along the radius towards the center. A centripetal force does no work.
F = mv2/r = mrω2
- Centrifugal force:- Centrifugal force is the fictitious force which acts on a body, rotating with uniform velocity in a circle, along the radius away from the center. Magnitude of centrifugal force is,
F = mv2/r
- Centripetal and centrifugal forces are equal in magnitude and opposite in direction. They cannot be termed as action and reaction since action and reaction never act on same body.
- Moment of Inertia (Rotational Inertia ‘I’) :- Moment of Inertiaof a body, about a given axis, is defined as the sum of the products of the masses of different particles constituting the body and the square of their distances from the axis of rotation. It depends upon two factors,
(i) Mass of body
(ii) Distribution of mass about the axis of rotation
(iii) Moment of inertia of a body should always be referred to as about a given axis, since it depends upon distribution of mass about that axis.
(iv) It does not depend upon the state of motion of rotating body. It is same whether the body is at rest, rotating slowly or rotating fast about the given axis.
I = ∑mr2
- Rotational Kinetic Energy:- Kr = ½Iω2 = ½ mr2ω2
So, I = 2Kr/ω2
- Radius Gyration:- Radius of gyration of a body about a given axis is that distance, at which if whole of the mass of the body were concentrated, it would have same moment of inertia as that of body.
I = MK2
So, K = √I/M
Again, Radius of gyration of a body about a given axis is defined as the square root of the mean of the squares of distances of various particles of the body from the axis of rotation.
So, K = √[r12+ r22+ r32+…./n]
- Center of mass for two particle system:-
(a) xCM=(m1x1+ m2x2)/(m1+ m2)
(b) vCM = (m1v1+ m2v2)/(m1+ m2)
(c) aCM = (m1a1+ m2a2)/(m1+ m2)
(d) vCM = dxCM/dt
(e) aCM = dvCM/dt = d2xCM/dt2
- System of mass for many particle system:-
xCM = ∑mixi / ∑mi
- Perpendicular axes theorem:- It states that the moment of inertia of a plane lamina, about an axis perpendicular to the plane lamina, is equal to the sum of the moments of inertia of the lamina about two mutually perpendicular axes lying in the plane of lamina and intersecting each other at the point where the perpendicular axis passes through the body.
I = Ix+Iy
- Parallel axes theorem:- It states that moment of inertia of a body, about an axis, is equal to the sum of the moment of inertia of the body about a parallel axis through its center of gravity and the product of the mass of body and the square of the distance between the two axes.
I = Ig+Mh2
Here, Ig is the moment of inertia of the body about an axis through its center of gravity G.
- Moments of Inertia of Various Objects:-

- Moment of inertia of a particle having mass m:-I = mr2
- Moment of inertia of a thin rod about an axis passing through its center and perpendicular to its length:-
? I =Ml2/12
- Moment of inertia of a ring about an axis passing through its center and perpendicular to its plane:-
(a) About one of its diameters:- Id = ½ (MR2)
(b)About a tangent
(i) Tangent lying in the plane of ring:-I = 3/2 (MR2)
(ii) Tangent perpendicular to the plane of ring:-I = 2MR2
- Moment of inertia of a solid disc:-
(a) About an axis passing through its center and perpendicular to its plane:- I = ½ MR2
(b) About one of its diameters:- Id = ¼ (MR2)
(c) About a tangent:-
(i) Tangent lying in the plane of disc:-I = 5/4 (MR2)
(ii) Tangent perpendicular to the plane of disc:- I = 3/2 (MR2)
- Moment of inertia of an annular disc:-
(a) About an axis passing through the center and perpendicular to the plane:-
(i) For a solid disc:- I = ½ MR2
(ii) For ring:- I = MR2
(b) About any of its diameter:-
(i) For a solid disc:- Id = ¼ (MR2)
(ii) For ring:- Id = ½ MR2
(c) About a tangent:-
(i) Tangent lying in the plane of disc:-
(1)For a solid disc:-I = 5/4 MR2
(2)For a ring:-I = 3/2 MR2
(ii) Tangent perpendicular to the plane of the disc:-
(1) For a solid disc:- I = 3/2 MR2
(2) For a Ring:- I = 2MR2
- Torque (τ) in vector form:-
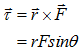
- Relation Between Moment of inertia (I) and Torque (
 ?) [Roatational Law of Accelaeration]:-
?) [Roatational Law of Accelaeration]:-
? ? = Iα
? = Iα
 ? = Iα
? = Iα
Here α is the angular acceleration.
- Newton’s law in rotational motion:-
(a) First Law:- It states that everybody continues in its state of rest or of uniform rotational motion about a given axis unless it is completed by some external unbalanced torque to change that state.
(b) Second Law:- It states that the rate of change of angular momentum of a body is directly proportional to the impressed torque and takes place in the direction of torque. Mathematically,  = Iα.
= Iα.
 = Iα.
= Iα.
(c) Third Law:- It states that to every torque there is an equal and opposite torque.
- Angular Momentum (L):-
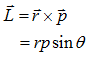
- Moment of Inertia (I) and Angular momentum (L):-
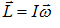
- Law of conservation of angular momentum:- The net angular momentum of an isolated system (no external torque), always remains constant.?
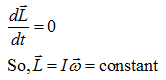
I1ω1=I2ω2
- Motion of a point mass attached to a string would over a cylinder capable of rotating about its axis of symmetry:-
Tension, T = mg/[1+(mR2/I)]
- Motion of a body rolling down an inclined plane without slipping:-
The maximum allowed angle for rolling without slipping.
(a) A cylinder rolling down the plane,
θmax = tan-1(3µ)
(b) A sphere rolling down the inclined plane,
θmax = tan-1[7/2 (µ)]
(c) A ring rolling down the inclined plane,
θmax = tan-1(2µ)
Here µ is the coefficient of sliding friction.
- Angular impulse:-

- Rotational work done:- W =τ?θ =τavθ
- Rotational power:-

- Kinetic Friction:-Kinetic friction is the force of friction which comes into play between two surfaces when there is some relative motion between them. The magnitude of force of kinetic friction fk (kinetic frictional force) is proportional to the normal force N.
?So fk = µk N
Here µk is the coefficient of kinetic friction.
Thus, coefficient of kinetic friction, µk = fk/N
- Rolling Friction:-Force of friction which comes into play, between two surfaces, while one is rolling over the other is called rolling friction. Rolling friction is similar to kinetic friction.
So,fr = µr N
Here µr is the coefficient of rolling friction and N is the normal force.
Thus, coefficient of rolling friction, µr = fr/N
for notes of thermal property: 1
for notes on laws of motion :2
Revision Notes on Gravitation and Projectile: 3Revision Notes on Circle:4
straight lines revision notes:5
hydrocarbons revison notes :6
some basic concepts of chemstry revision notes:7
si units : 8
M.s dhoni great captian: 9
virat kholi is a great cricketer:10
written by arpan ruhil


.jpg)
